My research goals are to develop structure-preserving numerical methods and to understand their fundamental properties, with the aim at improving long-term prediction and accuracy. Currently, I work on conservative discretizations for ordinary and partial differential equations arising from the Mathematical Sciences. I am also interested in their applications to a wide range of areas, such as in dynamical systems, many-body problems, geophysical flow, mathematical modelling, computational statistics, and machine learning.
Below are some recent work with my collaborators and students. For more details, see the list of publications.
Theoretical Developments of Conservative Methods
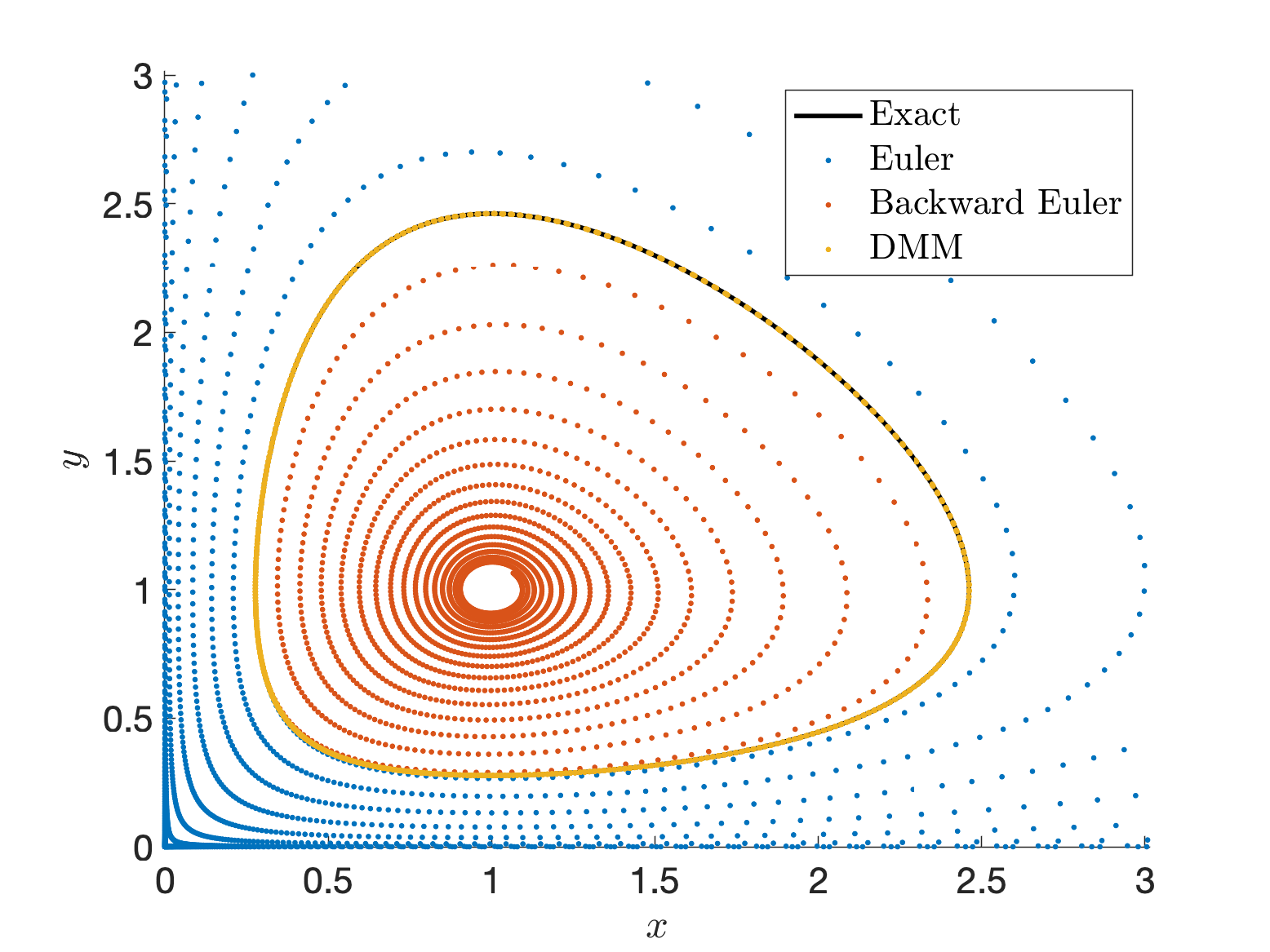
Conservative Methods for Dynamical Systems
with A. Bihlo and J.-C. Nave
We introduced the Discrete Multiplier Method (DMM) as a novel systematic approach to construct conservative finite difference schemes for quasilinear first-order ODEs with multiple conserved quantities of arbitrary forms. We derived discrete conditions for consistent conservative schemes of arbitrary order and devised various novel conservative schemes, including Hamiltonian systems, Poisson systems and dissipative systems.
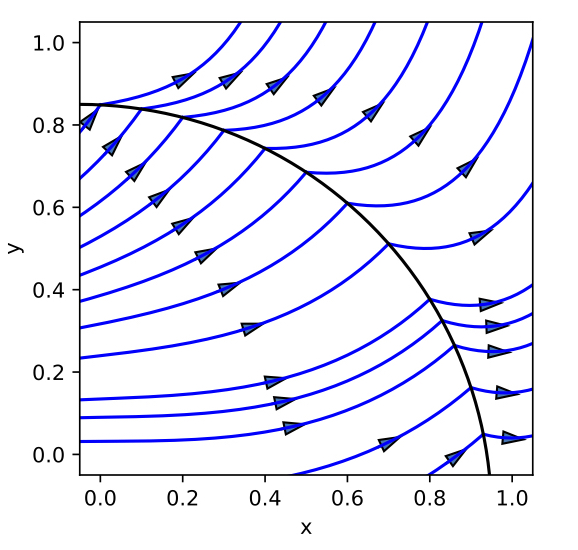
On the arbitrarily long-term stability of conservative methods
with J.-C. Nave
Symplectic methods possess favourable long-term properties, such as near conservation of energy over exponentially long time and at most linear growth in global error for completely integrable systems. In this work, we showed that under appropriate conditions, the global error of conservative methods is bounded for an arbitrarily long time.
Applications of Conservative Methods
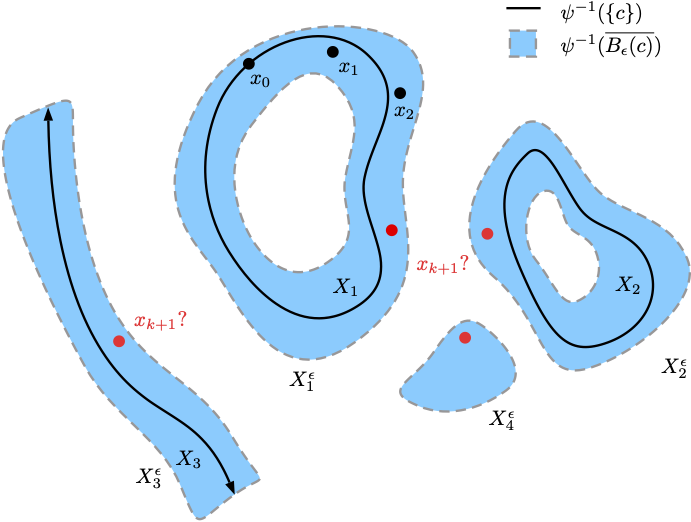
Conservative Integrators for Piecewise Smooth Systems with Transversal Dynamics
with A. Hirani and N. Wojtalewicz
Piecewise smooth dynamical systems arise naturally in many mechanical systems, electrical circuits and biological gene networks. These are smooth dynamical systems defined on multiple regions of the phase space separated by discontinuities along interfaces. In this work, we introduced a conservative transition scheme capable of preserving (possibly different) conserved quantities for piecewise smooth systems and we showed that the accuracy order can be preserved after crossing an interface.
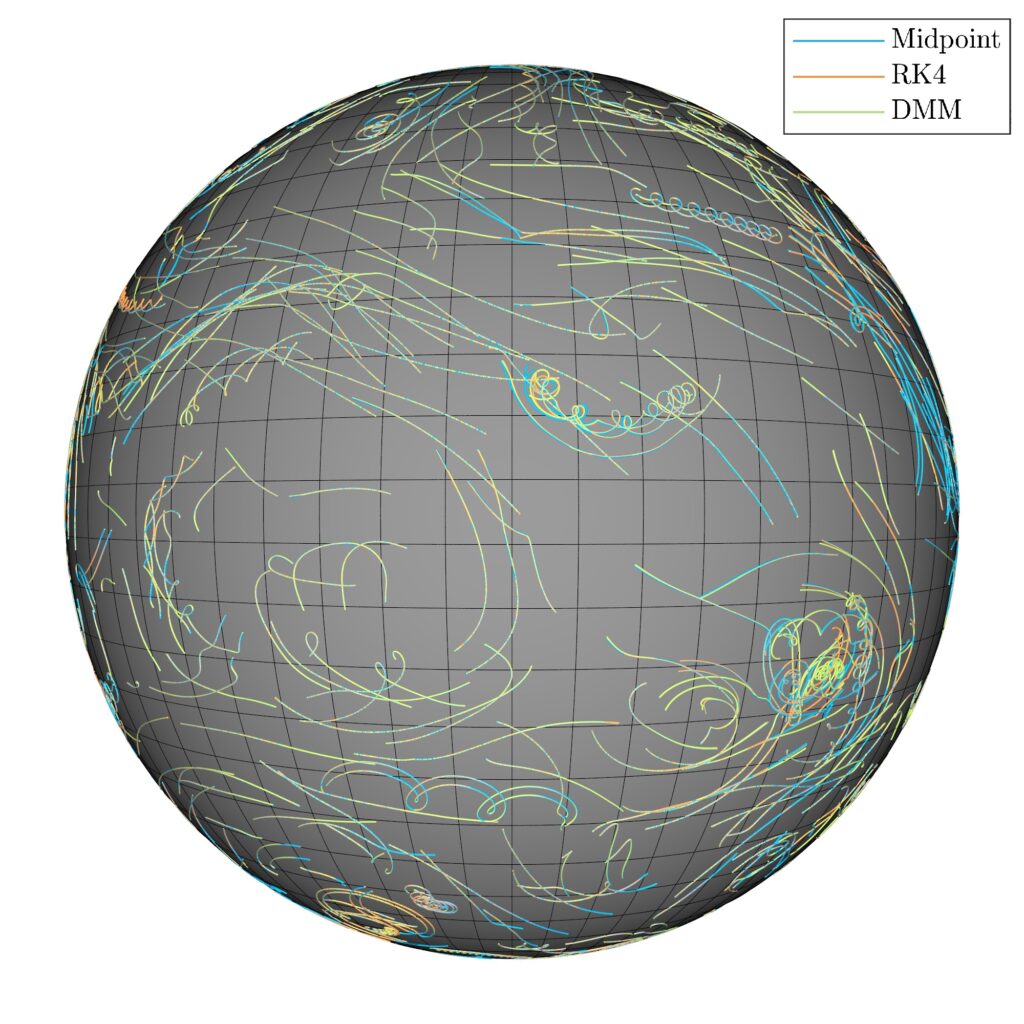
Conservative Integrators for Many-body Problems
with A. Bihlo and J.-C. Nave
Using DMM, we demonstrate conservative methods can be derived for many-body problems with multiple conserved quantities. In particular, we derive novel conservative second-order schemes for many-body problems, including n-species Lotka-Volterra system, n-body problem with radially symmetric potential, n-point vortex model in the plane and on the unit sphere.
Scientific Computing and Mathematical Modelling
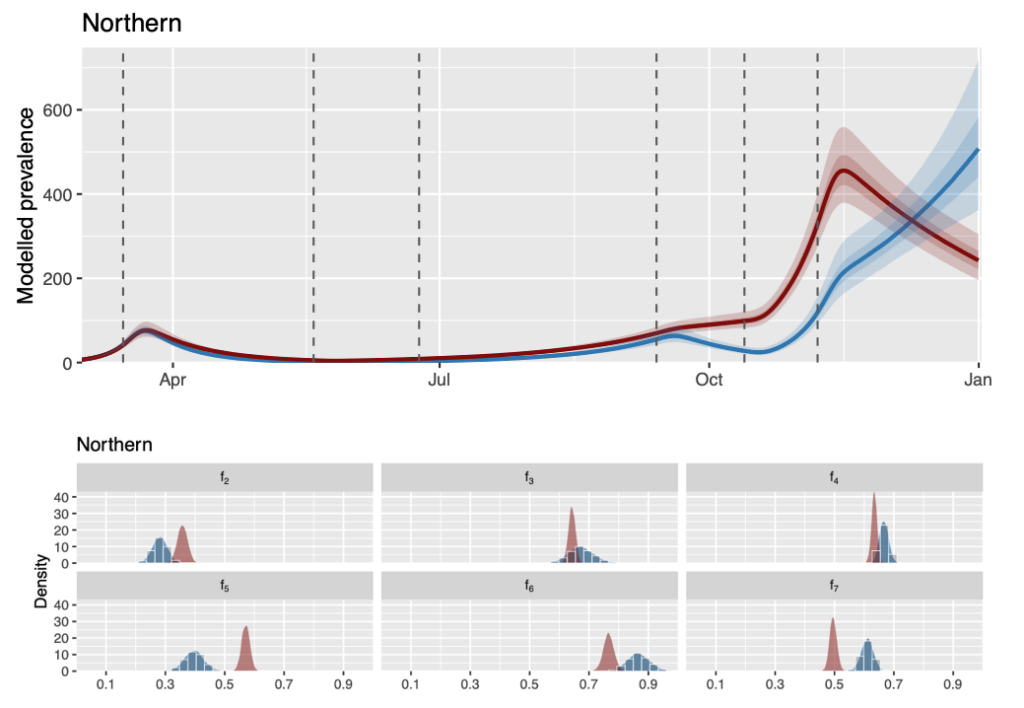
Assessing the effectiveness of regional physical distancing measures of COVID-19 in rural regions of British Columbia
with G. McGregor, J. Tippett, M. X. Wang, and S. W. K. Wong
In British Columbia (BC), early modelling efforts on the spread of COVID-19 with physical distancing measure were based on data and parameters from the most populous region of the province. In this work, we propose a hierarchical Bayesian model for each of the five health regions of BC and study the effectiveness of regional physical distancing measures using a Hamiltonian Monte Carlo approach.
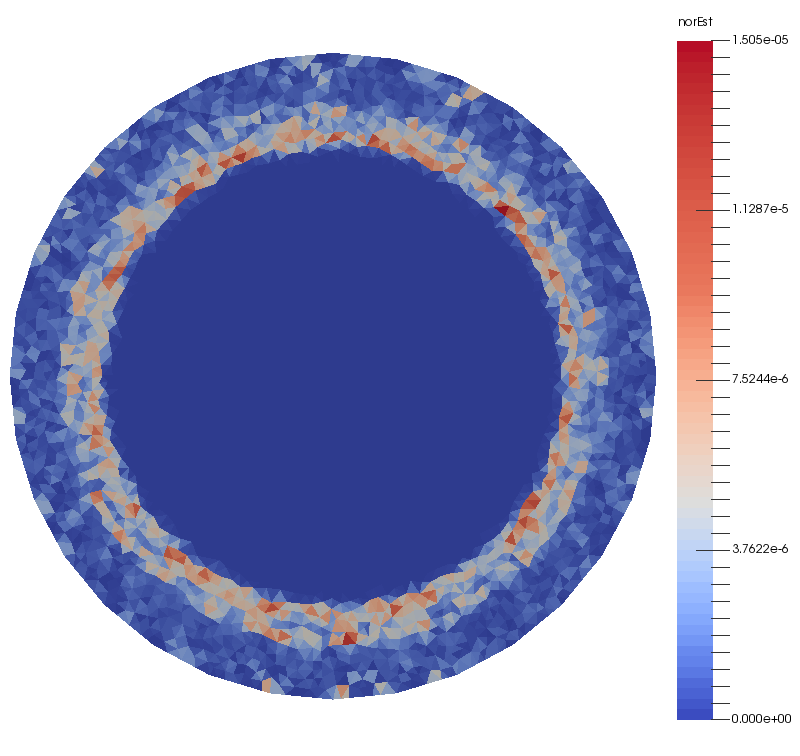
A posteriori error estimation for the p-curl problem
with M. Laforest
In applied superconductivity, a nonlinear Maxwell’s problem called the “p-curl problem” is used to model dynamics of the magnetic field in high temperature superconducting devices. Due to the nonlinearity of the p-curl problem, sharp moving fronts in the current density can arise. To accurately and efficiently resolve these moving fronts, we devised an adaptive finite element method using Nedelec elements with a posteriori error estimators for the p-curl problem and proved its reliability in the semi-discrete setting.
Funding Support
